Rule Solver – Miss Manners with Violations  

Rules as Preferences (Miss Manners Advanced). In the real world not all rules can be satisfied and we may consider them as preferences. For example, our June-2023 Challenge “Miss Manners” used a well-tuned data with equal numbers of males and females at each party. Of course, real data is not like this, but we still want to help Miss Manners to seat all guests while sticking to her rules as much as possible. So, the seating arrangement “boy-girl-boy-girl and each guest has someone on the left or right with a common hobby” becomes not a Rule but a Preference. New datasets for parties with 16, 32, 64, and 128 guests in this Excel file.

Implementation. This is a typical constraint satisfaction problem which could be easily represented and resolved by any Constraint Solver. Here is how this problem can be represented and solved using the latest OpenRules Rule Solver.

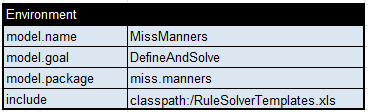
Problem Definition. Let’s start with the provided test data for the party of 16 guests converted to the OpenRules format in Excel file MissMannersPreferencesTest.xls:

Here is the corresponding business Glossary:

Thus, for each Guest we know Name, Gender, and Hobbies. Our goal is to define a Guest’s Seat for all Guests while satisfying as many Gender and Hobby rules (constraints) as possible.

We will assume that seats are numbered from 1 to 16, 32, 64, or 128. The Last Seat is calculated in the above Glossary as a number of elements in the array of Guests.

We will use the following top-level decision “Define” for the Problem Definition:

For each Guest, we will define the array “Seat Tags” with unique guests tags such as “1 Seat”, “2 Seat”, etc. It can be done using the regular OpenRules decision table:

Here “{{Name of Guest}}” will be opened by OpenRules using the current Guest’s name.

Then we will create the array “Seat Variables” with unknown decision variables for each guest seat that could take values from 1 to Last Seat:

Now we should be able to define all Gender and Hobby rules by posting the proper constraints on these yet unknown decision variables, and then use a standard search strategy to find the proper seats.

First of all, all Seat Variables should take different values from 1 to Last Seat. We also may assume the the first guest is always sitting at the first seat (as all other decision will be simply symmetrical). We may express these constraint in the following table:

To post Gender and Hobby constraints we need to consider all possible pairs of Guests (G1;G2) and state that G1 and G2 should have opposite genders and at least one common hobby. We can do it by executing incompatibility rules for each pair of different guests. We will use the predefined OpenRules “ActionNestedLoops” to iterate over different pairs of guests (G1;G2) inside the array of all “Guests”:

This iteration process will use several intermediate decision variables which we may define in the following temporary glossary:

The decision “SeatingForTwoGuests” will be executed for each pair of guests (G1;G2) assigning temporary names Guest1 and Guest2 and executing the rules “CreateSeatingViolations”:

This second table calls “Seating Violations” if G1 and G2 have the same Gender (rule 1) or their Hobbies do not intersect (rule 2). Here we also added the rules that removes possible symmetries to expedite the execution:

Here is the most complex decision “Seating Violations”:

This decision first will defines constrained variables for seats on left and right of the Guest1:

Here OpenRules will replace {{Guest1}} and {{Guest2}} with the actual names of Guest1 or Guest2.

Then the table “DefineConstraints” will create incompatibility constraints such as “Guest2 not Left of Guest1”, “Guest1 at First Seat”, etc. However, we cannot post them unconditionally but rather use them later:

And finally, the table “DefineSeatingViolations” will post soft constraints that could be potentially be violated:

All 4 of these constraints have the same importance “1” and saved in the array of constraints called “Seating Violations”.

And to complete Problem Definition we will define “Total Seating Violations”, a constrained variable which we want to minimize:

Problem Resolution. We may rely on the predefined search strategy “SolverMinimize” to minimize Total Seating Violations:

It will be invoked from our main sub-decision “Solve”:

However, after doing experiments with this problem, we found that for a large size problems like 128 guests it is difficult for Rule Solver to proved in reasonable time that it cannot find a better solution. So, we decided to limit the objective by posing the following constraint before the actual search:

And after the search we call the following table “SaveSolution” to assign the found solutions to all Guest’s decision variables {{Name of Guest}}Seat and to print the found solutions:

Main Decision. The will rely on the standard RuleSolver method “DefineAndSolver” to invoke both decisions “Define” and “Solve” as defined by the property “model.goal” in the Environment table:

Here is the automatically generated Decision Diagram:

As you can see, all decision modeling efforts were on problem definition and we don’t have to worry about problem resolution.

Execution Results. Running this decision model produced the following results:

Party of 16 Guests:

Party of 32 Guests:

Party of 64 Guests:

1 Seat[1] 2 Seat[2] 3 Seat[3] 4 Seat[5] 5 Seat[7] 6 Seat[9] 7 Seat[4] 8 Seat[11] 9 Seat[13] 10 Seat[15] 11 Seat[17] 12 Seat[6] 13 Seat[19] 14 Seat[21] 15 Seat[23] 16 Seat[8] 17 Seat[10] 18 Seat[25] 19 Seat[12] 20 Seat[14] 21 Seat[27] 22 Seat[29]

23 Seat[16] 24 Seat[18] 25 Seat[20] 26 Seat[31] 27 Seat[22] 28 Seat[33] 29 Seat[24] 30 Seat[26] 31 Seat[35] 32 Seat[37] 33 Seat[39] 34 Seat[28] 35 Seat[30] 36 Seat[41] 37 Seat[43] 38 Seat[32] 39 Seat[45] 40 Seat[34] 41 Seat[47] 42 Seat[49]

43 Seat[51] 44 Seat[53] 45 Seat[55] 46 Seat[36] 47 Seat[57] 48 Seat[38] 49 Seat[59] 50 Seat[61] 51 Seat[40] 52 Seat[63] 53 Seat[42] 54 Seat[44] 55 Seat[46] 56 Seat[48] 57 Seat[50] 58 Seat[52] 59 Seat[54] 60 Seat[56] 61 Seat[58] 62 Seat[60] 63 Seat[62] 64 Seat[64]

Elapsed time 955.49 milliseconds

Party of 128 Guests:

1 Seat[1] 2 Seat[2] 3 Seat[4] 4 Seat[3] 5 Seat[5] 6 Seat[6] 7 Seat[8] 8 Seat[7] 9 Seat[9] 10 Seat[11] 11 Seat[13] 12 Seat[10] 13 Seat[12] 14 Seat[15] 15 Seat[17] 16 Seat[19] 17 Seat[21] 18 Seat[14] 19 Seat[23] 20 Seat[25] 21 Seat[27]

22 Seat[29] 23 Seat[16] 24 Seat[18] 25 Seat[31] 26 Seat[33] 27 Seat[35] 28 Seat[20] 29 Seat[22] 30 Seat[37] 31 Seat[39] 32 Seat[24] 33 Seat[28] 34 Seat[41] 35 Seat[26] 36 Seat[43] 37 Seat[30] 38 Seat[32] 39 Seat[45] 40 Seat[47] 41 Seat[40] 42 Seat[49] 43 Seat[51]

44 Seat[34] 45 Seat[53] 46 Seat[55] 47 Seat[57] 48 Seat[36] 49 Seat[59] 50 Seat[61] 51 Seat[63] 52 Seat[38] 53 Seat[42] 54 Seat[60] 55 Seat[65] 56 Seat[67] 57 Seat[44] 58 Seat[69] 59 Seat[46] 60 Seat[48] 61 Seat[71] 62 Seat[50] 63 Seat[52] 64 Seat[54] 65 Seat[73]

66 Seat[56] 67 Seat[58] 68 Seat[75] 69 Seat[77] 70 Seat[62] 71 Seat[79] 72 Seat[81] 73 Seat[64] 74 Seat[66] 75 Seat[68] 76 Seat[70] 77 Seat[83] 78 Seat[85] 79 Seat[72] 80 Seat[87] 81 Seat[89] 82 Seat[91] 83 Seat[74] 84 Seat[93] 85 Seat[76] 86 Seat[95] 87 Seat[97]

88 Seat[99] 89 Seat[78] 90 Seat[101] 91 Seat[80] 92 Seat[82] 93 Seat[84] 94 Seat[86] 95 Seat[88] 96 Seat[103] 97 Seat[90] 98 Seat[105] 99 Seat[98] 100 Seat[107] 101 Seat[92] 102 Seat[94] 103 Seat[109] 104 Seat[111] 105 Seat[96] 106 Seat[100] 107 Seat[102] 108 Seat[104]

109 Seat[108] 110 Seat[113] 111 Seat[110] 112 Seat[106] 113 Seat[112] 114 Seat[115] 115 Seat[117] 116 Seat[119] 117 Seat[114] 118 Seat[116] 119 Seat[121] 120 Seat[123] 121 Seat[118] 122 Seat[125] 123 Seat[127] 124 Seat[120] 125 Seat[122] 126 Seat[124] 127 Seat[126] 128 Seat[128]

Elapsed time 16,411.42 milliseconds

The proper standard project is available in openrules.solver/MissMannersPreferences.